1、GBDT模型介绍；
2、GBDT回归算法
3、GBDT分类算法
4、GBDT的损失函数
5、正则化
6、GBDT的梯度提升与梯度下降法的梯度下降的关系；
7、GBDT的优缺点
1、GBDT模型介绍；
GBDT(Gradient Boosting Decision Tree) 又名：MART（Multiple Additive Regression Tree)
适用于分类和回归问题；
加法模型（基分类器的线性组合）
根据当前损失函数的负梯度信息来训练新加入的弱分类器，再将训练好的弱分类器以累加的形式结合到现有模型；
以决策树为基学习器的提升方法；一般会选择为CART（无论用于分类还是回归），也可以选择其他弱分类器的，选择的前提是低方差和高偏差，每次走一小步逐渐逼近结果的效果;
在训练过程中希望损失函数能够不断的减小，且尽可能快的减小。所以用的不是单纯的残差，而是损失函数的负梯度方向，这样保证每轮损失函数都在稳定下降，而且递减速度最快，类似于梯度下降法，来求损失函数的极小值；
Shrinkage（缩减）的思想认为，每次走一小步逐渐逼近结果的效果，要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树，它认为每棵树只学到了真理的一小部分，累加的时候只累加一小部分，通过多学几棵树弥补不足。
2、GBDT回归算法描述
步骤：
1、初始化：估计是损失函数极小化的常数值；
2、更新回归树：
数据――训练基分类器1――训练数据的伪残差――训练基分类器2――......
计算每个样本的损失函数在当前模型的负梯度值，将它作为残差的近似值，即新一轮的训练目标；
根据残差的近似值，求出使对应的损失函数的和最小的，第m棵回归树（第m个基分类器）$h(x_{i},\alpha )$，$\beta $相当于给梯度了一个步长；**先构造CART树，当CART树的结构定下来之后，再求叶子节点的值；
根据目标lable，求出使对应经验损失最小的参数$\rho $，来确认第m轮得到的基分类器，在最后的模型中的占比；
训练模型，直至误差小于要求，或树的个数为M时；
3、输出回归模型；
3、GBDT分类算法描述
GBDT分类算法和回归算法思路一样；但类别相减得到的残差并没有意义；
解决方案有两种方法：
一是用指数损失函数，此时GBDT算法退化为AdaBoost算法。
二是用类似于逻辑回归的对数似然损失函数的方法。也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。
此处介绍方法二，估计概率的方式；
1）二元分类
输入：训练数据集
，损失函数为
，y={-1，1} 输出：分类树
（1）初始化：
（2）对
： （a）对样本
，计算伪残差
（b）对概率残差
拟合一个分类树，得到第m棵树的叶节点区域
，
（c）对
，
，计算
**对于（b）(c)，这里拟合分类树应该还是首先遍历每个特征，然后对每个特征遍历它所有可能的切分点，然后对该分类树求使经验风险最小的切分及参数（就是叶节点区域的预测值）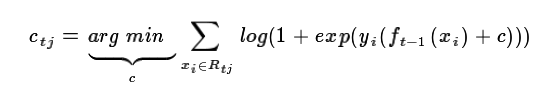
，由于这个式子比较难算，就用（c）来近似了。
（d）更新
（3）得到最终的分类树
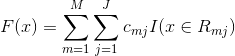
由于我们用的是类别的预测概率值和真实概率值的差来拟合损失，所以最后还要讲概率转换为类别，如下：
最终输出比较类别概率大小，概率大的就预测为该类别。
（用的损失函数使对数损失，所以这里用上面的式子来计算类别；
当y=1时，损失函数最小需要F(X)=正无穷，此时y=1的概率为1，y=0的概率为0；
当y=-1时，损失函数最小需要F(X)=负无穷，此时y=1的概率为0，y=0的概率为1；）
其实二元分类和回归的原理是一样的，只是把分类的lable改成了预测概率，再通过概率来预测类别；
2）多元分类
输入：训练数据集
，损失函数为
，
=｛0，1｝表示是否属于第k类别，1表示是，0表示否。
，表示共有多少分类的类别。 输出：分类树
相当于在训练的时候，是针对样本 X 每个可能的类都训练一个分类树。
（1）初始化：
，
（2）对
：
（a）计算样本点俗属于每个类别的概率：
（b）对k=1,2,...,K：zhi
1）
，
（这是根据损失函数和P（x）求导算出来的，体现了负梯度的概念） 2）对概率伪残差
拟合一个分类树 3）
（跟二分类一样，这也是一个近似计算方法） 4）
（3）得到最终的分类树（这是K类中的第k类的GBDT方法求出来的模型）
最后得到的
可以被用来去得到分为第k类的相应的概率
：
相当于对每一类都有一个求GBDT的概念，只是该类的预测值不仅与该类本身有关，还与剩余的K-1个GBDT模型的输出相关；
损失函数的求导：
对于第k类的第i个样本的损失函数为：
$L(y_{ki},f_{k}(x_{i}))=-\sum_{l=1}^{K}y_{li}\ln P_{li}$对于样本i来说，只有一个类别的y为1，其他的都是0,$\sum_{l=1}^{K}y_{li}=1$；
$P_{ki}=\frac{exp(f_{k}(x_{i}))}{\sum_{l=1}^{K}exp(f_{l}(x_{i}))}$
$L(y_{ki},f_{k}(x_{i}))=-\sum_{l=1}^{K}y_{li}\ln P_{li}=y_{ki}\ln P_{ki}+\sum_{l\neq k}^{}y_{li}\ln P_{li}=y_{ki}\ln \frac{exp(f_{k}(x_{i}))}{\sum_{l=1}^{K}exp(f_{l}(x_{i}))}+\sum_{l\neq k}^{}y_{li}\ln\frac{exp(f_{l}(x_{i}))}{\sum_{l=1}^{K}exp(f_{l}(x_{i}))} $
两项都有$f_{k}(x_{i})$,在分别求导会得到
当损失函数为平方损失函数时，即为残差； 提升树是GBDT的一种，即损失函数为平方损失函数时；
4、GBDT的损失函数
对于分类算法，其损失函数一般有对数损失函数和指数损失函数两种:
（1）exponential：指数损失，表达式如下：
（2）deviance：对数损失，类似于logistic回归的损失函数，输出的是类别的概率，表达式如下：
对于回归算法，常用损失函数有如下4种:
（1）平方损失，这是最常见的回归损失函数了，如下：
导数为y-f(x)，即 残差；
（2）绝对损失
对应负梯度为：
（3）huber损失，对于远离中心的异常点采用绝对损失，而中心附近的点采用平方损失。这个界限一般用分位数点度量。损失函数如下：
对应的负梯度为：
（4）quantile：分位数损失，它对应的是分位数回归的损失函数，表达式如下：
其中θ为分位数，需要我们在回归前指定。对应的负梯度为：
对于huber损失和分位数损失主要作用就是减少异常点对损失函数的影响。
5、正则化
方法1：用v来调节补偿和迭代次数，通过选择最合适的v来减少迭代次数；
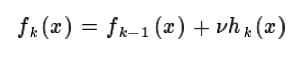
方法2：CART正则化剪枝
方法3：通过子采样比例（subsample），取值为(0,1]，每棵树训练的时候只选取全部数据的一部分训练，来防止过拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间。
注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。
例如：每棵树抽样的整体都是100个样本；随机森林抽样是放回的，最极端的可能全部都是重复，即一个样本；无放回抽样主要是样本不会重复；gbdt的子采样比例为0.8时，每棵树都会从100个样本中不放回的选择80个样本来训练；
6、GBDT的梯度提升与梯度下降法的梯度下降的关系；
GBDT VS 梯度下降
都是在每一轮迭代中，利用损失函数相对于模型的负梯度方向的信息对当前模型进行更新；
梯度下降中，模型是以参数化形式表示，更新模型相当于更新参数；
GBDT中，模型不需要进行参数化表示，直接定义在函数空间，扩展了可以使用的模型种类；
7、GBDT的优缺点
1、效果确实挺不错。
2、即可以用于分类也可以用于回归。
3、可以筛选特征。（不相关的特征可以不用）
4、可以很好的处理缺失特征的数据，因为决策树的每个节点只依赖一个 feature，如果某个 feature 不存在，这颗树依然可以拿来做决策，只是少一些路径。像逻辑回归，SVM 就没这个好处。
5、可以很好的处理各种类型的特征，包括连续值和离散值，同样逻辑回归和 SVM 没这样的天然特性。
7、数据规模影响不大，因为我们对弱分类器的要求不高，作为弱分类器的决策树的深度一般设的比较小，即使是大数据量，也可以方便处理。像 SVM 这种数据规模大的时候训练会比较麻烦。
8、数据不需要归一化，特征的作用只是用来分裂结点，叶结点的值与特征值大小无关，是否归一化并不影响叶结点值的大小，也不影响梯度下降的进程；
9、在相对少的调参时间情况下，预测的准确率也可以比较高；
3-8都是决策树本身的优势。
缺点
由于弱学习器之间存在依赖关系，难以并行训练数据。
https://blog.csdn.net/qq_24519677/article/details/82020863
https://www.cnblogs.com/ModifyRong/p/7744987.html
来源：博客园
作者：DanniX
链接：https://www.cnblogs.com/danniX/p/10628980.html