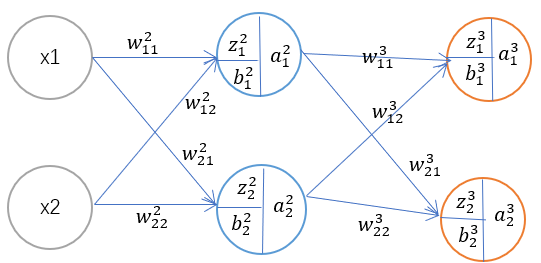
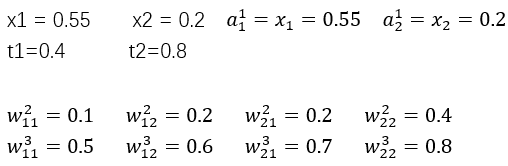
反向传播四公式:
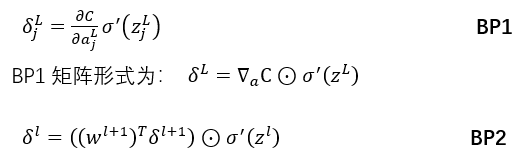

反向传播的最终目的是求得使代价C最小时w、b的最佳值,为了方便计算引入了神经单元误差δ_j^l,其定义为误差C关于某个神经单元z的关系;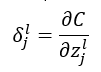
其定义如上所示,某神经元误差为代价C(总误差)关于z的偏导数,其中l为神经网络的层数,j为第几个神经元;
这里的代价函数(损失函数)使用的是平方误差,因此C等于: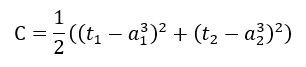
BP1
此公式用于求神经网络最后一层神经元的误差,下面通过BP1公式用于求最后一层神经元(输出层)中第一个神经元的误差;
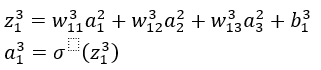
根据链式法则由此可得到上诉四个公式中得前面BP1
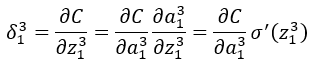
BP1中得L为神经网络得最后一层,而在我们此网络中最后一层为3,所以此处L=3;
BP2
BP2与BP1类似,不同得是BP1用于求最后一层神经元误差,而BP2则是用于求L层前面某一层得神经元误差,下面通过BP2公式用于求第二层神经元中的第一个神经元的误差;
同样我们也可通过链式法则得出:
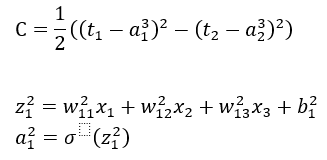
有:
因此可以得: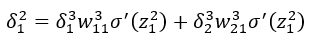
将公式转换为矩阵模式,第2层神经元得误差为: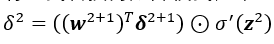
我们将BP1与BP2带入即可得到BP3与BP4;
通过BP1与BP2公式即可通过BP3、BP4轻松得到w与B;
BP3
此公式用于求误差C关于某个权重的偏导数,在求得BP2后此处只需吧BP2带入到公式即可求得BP3;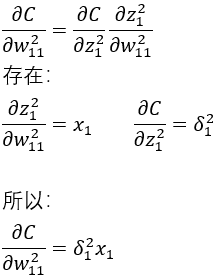
BP4
求误差C关于偏置b的偏导数,BP4与BP3一样得到BP2即可带入得出BP4;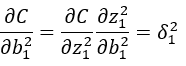
反向传播算法给出了一种用于计算代价函数(损失函数)梯度得方法,具体步骤如下:

1、计算第二层
矩阵形式:
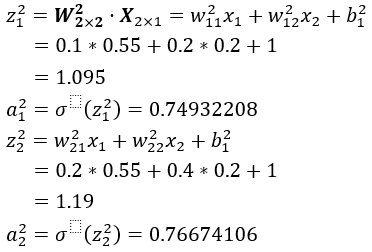
2、计算第三层
矩阵形式:

当前使用的为平方损失函数(代价函数);
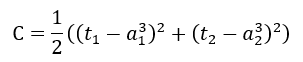
矩阵形式: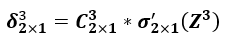
输出层第一个神经元误差δ_1^3:
输出层第一个神经元误差δ_2^3: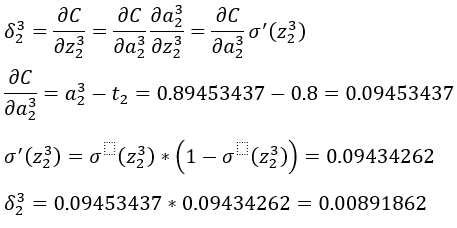
矩阵形式:
此处用的是BP3与BP4公式,在计算出BP1与BP2后将其带入到公式中即可计算出C关于w、b的梯度;
矩阵形式:
矩阵形式:
更新w、b公式: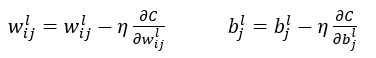
在计算出误差C关于每个权重每个偏置的偏导数后再使用得到的值带入上述公式更新每一个w、b即可,在更新完成w、b后如误差达到指定精度或epochs则继续执行上述的2-5步骤直到误差满意或指定epochs为止;