//7.18前三天的等我周日再继续复习总结orz_(:з」∠)_每一天都是充实的欧
7.15:差分与前缀和
7.16: 倍增与ST表
7.17:并查集进阶
7.18:树状数组与线段树
树状数组:
1.引入lowbit(x)
int lowbit(int i)
{
}-11=(0100+1)=0101
&1011
树状数组 c[x],比如c[4],4的二进制是(100),100刚好是3位数,所以这个树状数组到c[4]为止高度是3。
除了树根,c[x]的父节点为 c[x+lowbit(x)]
能用树状数组尽量用树状数组,快,省空间。(一般用来单点更新,区间求和,维护最大值二不能维护最小值。但是求区间最大值的时候复杂度比较高容易TLE,这个时候还是需要用到线段树)
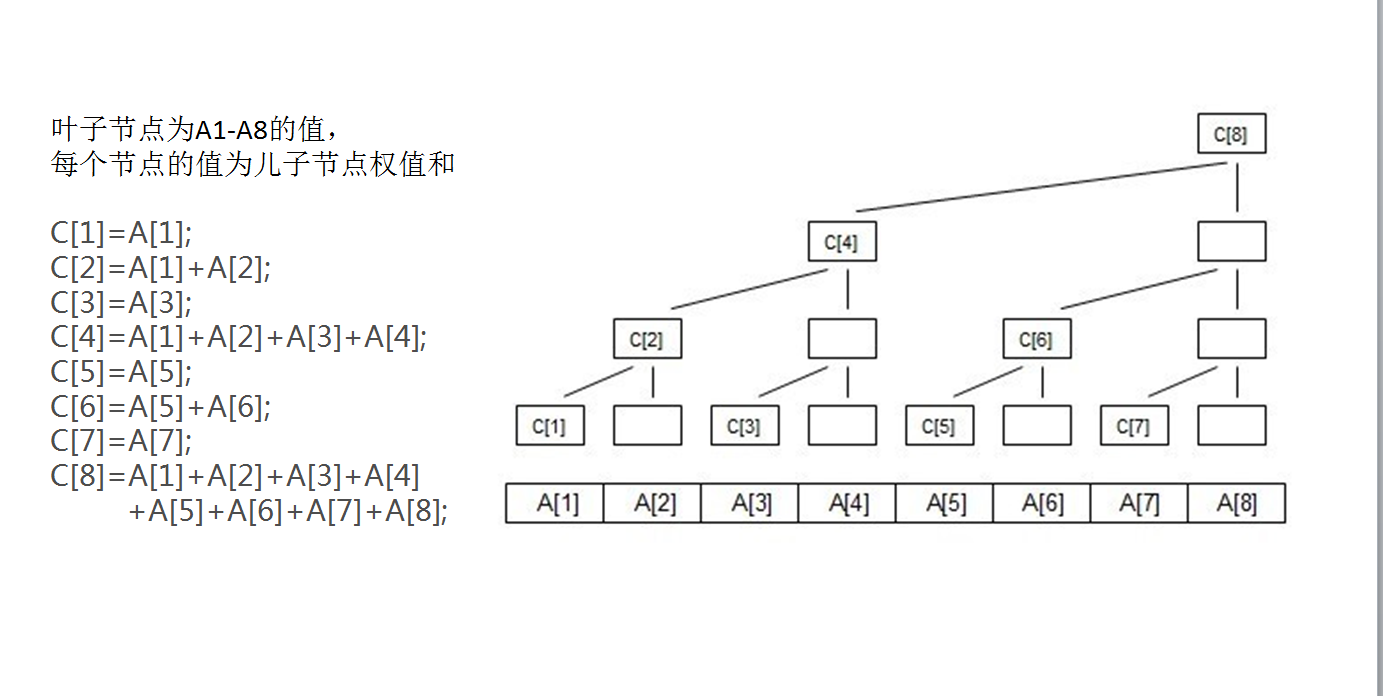
“细细观察二进制 树状数组追其根本就是二进制的应用”


1 #include<bits/stdc++.h> 2 using namespace std; 3 const int M =100000+100; 4 int n,t; 5 int a[M],C[M]; 6 int lowbit(int x) 7 { 8 return x&(-x); 9 } 10 int sum(int x) 11 { 12 int ret=0; 13 while(x) 14 { 15 ret+=C[x]; 16 x-=lowbit(x); 17 } 18 return ret; 19 } 20 void updata(int x,int d) 21 { 22 while(x<=n) 23 { 24 C[x]+=d; 25 x+=lowbit(x); 26 } 27 } 28 int main() 29 { 30 scanf("%d",&t); 31 32 for(int i=1;i<=t;i++) 33 { 34 printf("Case %d:\n",i); 35 scanf("%d",&n); 36 for(int i=1;i<=n;i++) 37 C[i]=0; 38 for(int i=1;i<=n;i++) 39 { 40 scanf("%d",&a[i]); 41 updata(i,a[i]); 42 } 43 char s[10]; 44 while(scanf("%s",s)&&s[0]!='E') 45 { 46 int q,w; 47 scanf("%d%d",&q,&w); 48 if(s[0]=='A') 49 updata(q,w); 50 else if(s[0]=='S') 51 updata(q,-w); 52 else 53 printf("%d\n",sum(w)-sum(q-1)); 54 } 55 } 56 return 0; 57 } 

1 #include<iostream> 2 #include<cstdio> 3 //#include<bits/stdc++.h> 4 using namespace std; 5 typedef long long ll; 6 const int M = 100000+100; 7 ll a[M]; 8 ll sum[M]; 9 ll c[2][M]; 10 int n; 11 int lowbit(int x) 12 { 13 return x&(-x); 14 } 15 void add(int x,int d,int k) 16 { 17 while(x<=n) 18 { 19 c[k][x]+=d; 20 x+=lowbit(x); 21 } 22 } 23 ll ask(int x,int k) 24 { 25 ll ans=0; 26 while(x) 27 { 28 ans+=c[k][x]; 29 x-=lowbit(x); 30 } 31 return ans; 32 } 33 int main() 34 { 35 int q; 36 cin>>n>>q; 37 for(int i =1 ;i <= n;i++) 38 { 39 scanf("%I64d",&a[i]); 40 sum[i]=sum[i-1]+a[i]; 41 // cout<<sum[i]<<endl; 42 } 43 char s[2]; 44 int l,r; 45 ll ans=0; 46 for(int i = 1; i <=q; i++) 47 { 48 scanf("%s%d%d",s,&l,&r); 49 if(s[0]=='C') 50 { 51 int d; 52 scanf("%d",&d); 53 add(r+1,-d,0),add(r+1,-(r+1)*d,1); 54 add(l,d,0),add(l,l*d,1); 55 } 56 else 57 { 58 ans=sum[r]+(r+1)*ask(r,0)-ask(r,1); 59 ans-=sum[l-1]+l*ask(l-1,0)-ask(l-1,1); 60 printf("%I64d\n",ans); 61 } 62 } 63 return 0; 64 } 线段树:
满足区加法。
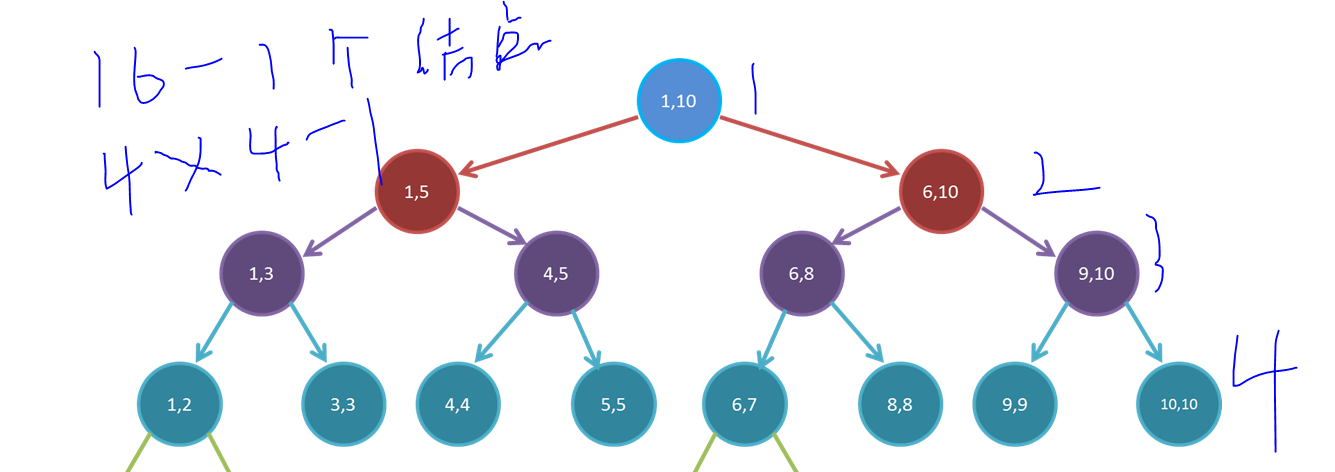
当build建树的时候,是先向下递归,再从下到上逐步更新。


1 /* 2 区间更新 求区间和 3 */ 4 //#include<bits/stdc++.h> 5 #include<cstdio> 6 #include<iostream> 7 #include<cstring> 8 #include<algorithm> 9 typedef long long ll; 10 using namespace std; 11 #define maxn 100000+100 12 ll sum[maxn<<2]; 13 ll lazy[maxn<<2]; 14 //int a[maxn<<2]; 15 void build(int l,int r,int rt) 16 { 17 lazy[rt]=0; 18 if(l==r) 19 { 20 scanf("%lld",&sum[rt]); 21 return; 22 } 23 int mid=(l+r)/2; 24 build(l,mid,rt<<1); 25 build(mid+1,r,rt<<1|1); 26 sum[rt]=sum[rt<<1]+sum[rt<<1|1]; 27 } 28 void pushdown(int l,int r,int rt) 29 { 30 if(lazy[rt]) 31 { 32 lazy[rt<<1]+=lazy[rt]; 33 lazy[rt<<1|1]+=lazy[rt]; 34 int mid=(l+r)/2; 35 sum[rt<<1]+=(mid-l+1)*lazy[rt]; 36 sum[rt<<1|1]+=(r-mid)*lazy[rt]; 37 lazy[rt]=0; 38 } 39 } 40 void change(int l,int r,int rt,int L,int R,int c) 41 { 42 if(L<=l&&r<=R) 43 { 44 lazy[rt]+=(ll)c; 45 sum[rt]+=(r-l+1)*(ll)c; 46 return; 47 } 48 pushdown(l,r,rt); 49 int mid=(l+r)/2; 50 if(R>mid) 51 change(mid+1,r,rt<<1|1,L,R,c); 52 if(L<=mid) 53 change(l,mid,rt<<1,L,R,c); 54 sum[rt]=sum[rt<<1]+sum[rt<<1|1]; 55 } 56 ll query(int l,int r,int rt,int a,int b) 57 { 58 if(l>=a&&r<=b) 59 return sum[rt]; 60 pushdown(l,r,rt); 61 int mid=(l+r)/2; 62 ll ans=0; 63 if(a<=mid) 64 ans+=query(l,mid,rt<<1,a,b); 65 if(b>mid) 66 ans+=query(mid+1,r,rt<<1|1,a,b); 67 return ans; 68 } 69 int main() 70 { 71 int t,n,K; 72 while(~scanf("%d%d",&n,&t)) 73 { 74 build(1,n,1); 75 char s[3]; 76 while(t--) 77 { 78 int a,b,c; 79 scanf("%s",s); 80 if(s[0]=='C') 81 { 82 scanf("%d%d%d",&a,&b,&c); 83 change(1,n,1,a,b,c); 84 } 85 else 86 { 87 scanf("%d%d",&a,&b); 88 printf("%lld\n",query(1,n,1,a,b)); 89 } 90 } 91 } 92 return 0; 93 } lazy标记的时候,记得访问后就顺便更新一波,再把最初的懒标记清空为0。
线段树的其他变形应用:逆序对,区间覆盖(把lazy+=d 改成lazy=d),区间最长序列和(区间合并),扫描线,求第k大的某物。
。。
7.19:线段树进阶
遇到了一道题,是poj的Ultra-QuickSort 归并排序。即给出一串数字,求出使用归并排序时数字交换的次数。
归并排序的数字交换次数刚好就是这串数字的逆序数。
例如:5 3 4 2 1
n=5,一共5个数字。
第三步:a[4]=1;因为4<n,所以计算一下从a[n]到a[4+1],那就是a[5],所以ans=1。
第四步:a[2]=1;同理 ans=a[5]+a[4]+a[3]=3;
第五步:a[1]=1;同理ans =a[5]+a[4]+a[3]+a[2]=4。
这里的ans可以开个树状数组记录一下。
代码应用:
2.线段树
离散化概念:一开始感觉离散化?nb啊,看不懂什么意思。。。又想起离散数学,心中感慨万千。
离散化是程序设计中一个非常常用的技巧,它可以有效的降低时间复杂度。其基本思想就是在众多可能的情况中“只考虑我需要用的值”。
这一步有点类似于数据分析,就是第一步清洗数据,否则可能会占用太多内存,garbage in ,garbage out。
所以可以先用vector暂时存一下数据,然后用unique去重,在减去首地址就是它的去重后的大小了。但是注意,vector 的目的并非存储本身,而是离散化。
然后,就像把数据按一定大小顺序重新排序这一步也是离散化。比如贪心。。。
吉司机线段树/势能线段树:


就是这样的题目,不能简单粗暴地用lazy标记,所以要改成 bool flag[i],以确定是否要进行开根号处理,因为这个数比如 153437757 它再大多开几次而且还是向下取整,它也很快就变成1了,所以暴力向下更新即可。据称不超过5次就变成1.
权值线段树:
用来找一棵树的前驱,后继,第k大的x,x是第k大。当然,这棵树还可以删除,插入数字。