今天,南外夏令营第一天打卡 , 咳咳,
概念:为了便于了解,如图(在一颗有根树中,有若干个子树):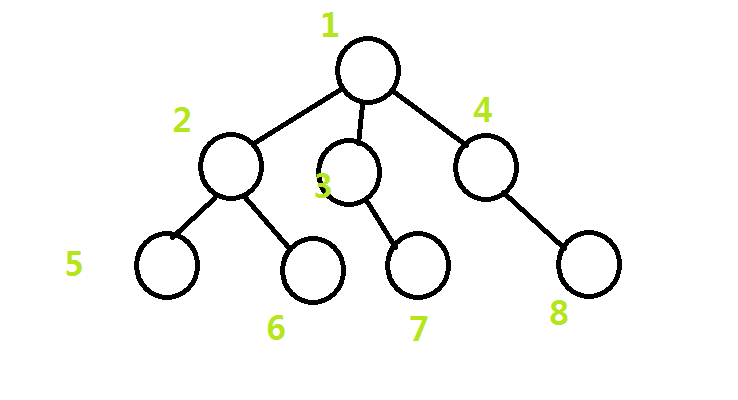
其中1号节点为该树的根,我们所谓的祖先即一个子树的根及其的根的根和其的根的根的根……(在LCA中包括子树本身)(其实不用那么绕口),举个例子(在本文之后直接用编号来称呼节点):
5的祖先:5、2、1;7的祖先:7、3、1;2的祖先:2、1……
而所谓的最近公共祖先为两个节点首先能找到的公共祖先(即深度最最大的公共祖先)
来个模版题()

下面就是激动人心的代码时刻让我们进行代码实现的步骤:
1、先从最简单的暴搜入手:通过链表(从根一直往下搜,标记父节点)
nlogn)


struct st{ int to,next; }edge[]; int hd[]; void add(int from,int to) { cnt++; edge[cnt].next=hd[from]; edge[cnt].to=to; hd[from]=cnt; } void DFS(int now,int d)找祖先 { deep[now]=d; for (int i=hd[now];i;i=edge[i].next) { fa[edge[i].to]=now; DFS(edge[i].to,d+1); } } void LCA() { if (deep[x]<deep[y])swap(x,y); while (deep[x]>deep[y])x=fa[x]; while (x!=y) { x=fa[x]; y=fa[y]; } ans=x;//或ans=y } 2、倍增算法(时间复杂度logn)
首先,我们需要一定的二进制的基础:
结论1:二进制的所有位只存在0或1,
这些次方一定不同,因为结论1得))
结论3:2j-1+2j-1=2j!
设f[i][j]:i号节点的第2j代的祖先编号,因为2j-1+2j-1=2j,所以一个节点的2j代的祖先是其2j-1代的祖先的2j-1的祖先,得f[i][j]=f[f[i][j-1]][j-1]
for (int i=maxn;i>=0;i--)//必须从小到大:因为5=22+20,而如果从小到大:20+21=3,但3+22>5,不能"悔棋"!!! { if (deep[f[x][i]]>=deep[y])x=f[x][i]; } 2、找共同祖先:
for (int i=maxn;i>=0;i--)//必须从小到大,同理 { if (f[x][i]!=f[y][i]) { x=f[x][i]; y=f[y][i]; } } return f[x][0]; 

struct st{ int to,next; }edge[]; int hd[],cnt,deep[],f[][],ans,n,m,s; int Find(int t) { int u=1; while ((u<<1)<=t)u<<=1; } void add(int from,int to) { cnt++; edge[cnt].next=hd[from]; edge[cnt].to=to; hd[from]=cnt; } void DFS(int now,int d) { deep[now]=d; int maxn=Find(d); for (int i=1;i<=maxn;i++) { f[now][i]=f[f[now][i-1]][i-1]; } for (int i=hd[now];i;i=edge[i].next) { f[edge[i].to][0]=now; DFS(edge[i].to,d+1); } } int LCA(int x,int y) { if (deep[x]<deep[y])swap(x,y); int maxn=Find(x); for (int i=maxn;i>=0;i--)//必须从小到大 { if (deep[f[x][i]]>=deep[y])x=f[x][i]; } if (x==y)return x; maxn=Find(y); for (int i=maxn;i>=0;i--)//必须从小到大 { if (f[x][i]!=f[y][i]) { x=f[x][i]; y=f[y][i]; } } return f[x][0]; }//仅供参考