需要完成的任务为包含简单幂函数和简单正余弦函数的导函数的求解。本次多项式求导具体包括以下因子:
- 常数因子:包含一个带符号整数,-002;
- 幂函数因子: x 、 x^-3;
- 表达式因子: (表达式);
- 三角函数因子:sin(因子) 、cos(因子) ^2.
因子组合成项:因子[*因子];
项组合成为表达式:项[±项];
要对输入的表达式进行解析,输出对应的导函数。
采用递归下降进行语法分析的思路,按照“表达式――>项――>因子”的顺序,将表达式分解到可以直接求得导数的因子,再逐层将因子的导数返回并组合成项和表达式的导数。
流程图如下: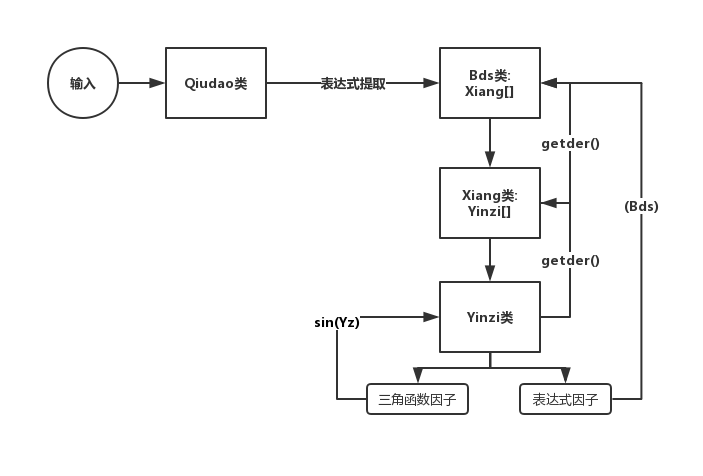
将输入作为第一个表达式: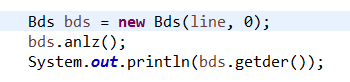
并输出该表达式的导函数作为最终结果。
表达式类进行解析拆分出项,项拆分出因子:
因子对象中进行语法分析,提取出第一个因子并返回解析进度给项对象。
特别地,在表达式因子解析时会新建一个表达式对象以分析括号内的内容:
与之相似,解析三角函数因子时括号内的因子部分也会新建一个因子对象进行解析: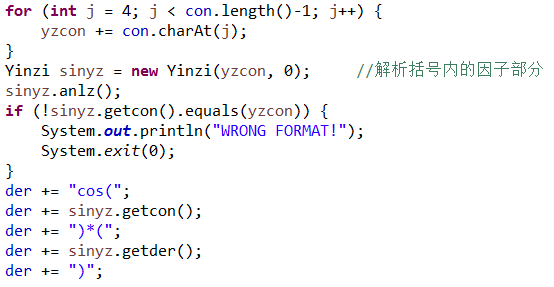
当一个项对其下的因子解析完成时,会得到该项的导函数: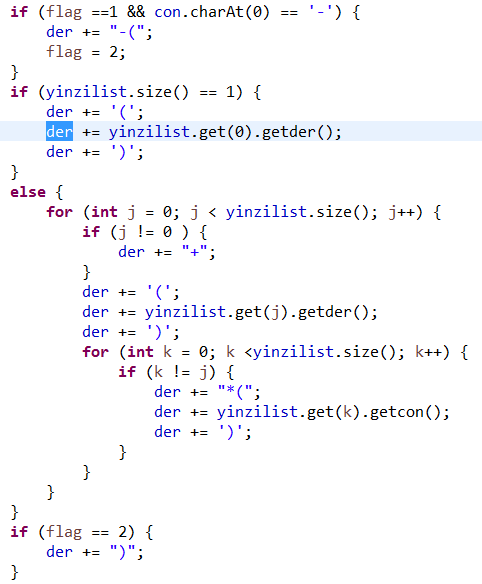
运用该求导公式结合各因子的内容和导函数即可: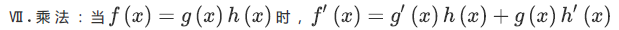
当一个表达式中的项都解析完成,表达式的导函数也将可求得: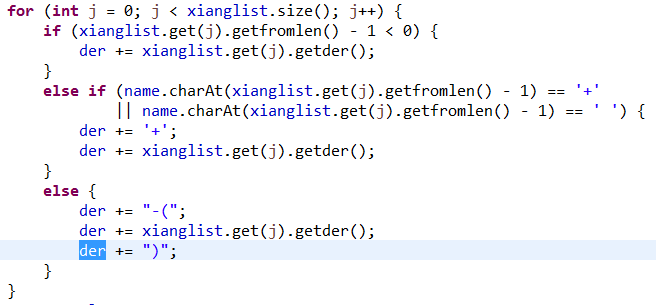
将各项的导函数与其前面的'+'或'-'号连接即可。