本篇文章假设你已有lstm和crf的基础。
BiLSTM+softmax
lstm也可以做序列标注问题。如下图所示: 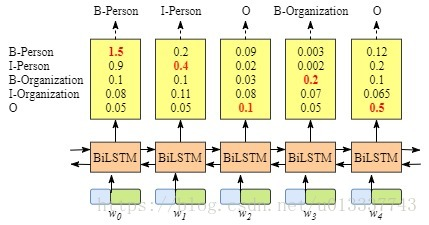
双向lstm后接一个softmax层,输出各个label的概率。那为何还要加一个crf层呢?
我的理解是softmax层的输出是相互独立的,即虽然BiLSTM学习到了上下文的信息,但是输出相互之间并没有影响,它只是在每一步挑选一个最大概率值的label输出。这样就会导致如B-person后再接一个B-person的问题。而crf中有转移特征,即它会考虑输出label之间的顺序性,所以考虑用crf去做BiLSTM的输出层。
BiLSTM+crf的基本思想
BiLSTM+crf的结构如图所示:

对于每一个输入我们得到一个预测label序列定义这个预测的得分为:
其中Pi,yi为第i个位置softmax输出为yi的概率,Ayi,yi+1为从yi到yi+1的转移概率,当tag(B-person,B-location。。。。)个数为n的时候,转移概率矩阵为(n+2)*(n+2),因为额外增加了一个开始位置和结束位置。这个得分函数S就很好地弥补了传统BiLSTM的不足,因为我们当一个预测序列得分很高时,并不是各个位置都是softmax输出最大概率值对应的label,还要考虑前面转移概率相加最大,即还要符合输出规则(B后面不能再跟B),比如假设BiLSTM输出的最有可能序列为BBIBIOOO,那么因为我们的转移概率矩阵中B->B的概率很小甚至为负,那么根据s得分,这种序列不会得到最高的分数,即就不是我们想要的序列。
BiLSTM+crf的训练
训练思想很巧妙。
首先我们需要训练的参数为:
1.BiLSTM中的参数
2.转移概率矩阵A
对于每个训练样本X,求出所有可能的标注序列y的得分S(X,y)(注意这里应该不用遍历所有可能的y,维特比算法应该用得上),对所有得分进行归一化:
这里分子上的y是正确标注序列(因为我们是一个有监督学习)
下面引出损失函数(虽然我感觉这不应该称为“损失”),对真实标记序列y的概率取log:
那么我们的目标就是最大化上式(即真实标记应该对应最大概率值),因为叫损失函数,所以我们也可以对上式取负然后最小化之,这样我们就可以使用梯度下降等优化方法来求解参数。在这个过程中,我们要最大化真实标记序列的概率,也就训练了转移概率矩阵A和BiLSTM中的参数。
BiLSTM+crf的预测
当模型训练完毕后,就可以去测试了。
预测的时候,根据训练好的参数求出所有可能的y序列对应的s得分(这里应该也可以利用维特比算法),然后取:
做为预测结果输出。
原文:https://blog.csdn.net/bobobe/article/details/80489303