流平衡分析（FBA）
Flux Balance Analysis
本文参考流平衡分析简介
流 （flux）
流就是代谢网络中化学反应的反应速率
在稳态下，各代谢物浓度不变，反应速率满足一定的分布（流分布）
分子类型转化流指单位时间内的转化量
平衡
平衡就是约束
约束来自两个方面：
- 基本物理规律的约束，物质不灭，能量守恒等
- 边界条件的约束，底物的供应量（上限），产物的生成量（下限）等
因此流平衡分析又称为基于约束的模型（constraint-based model）
线性规划问题
流平衡分析即线性规划问题（linear programming），在限制条件下求最优解
线性规划算法详解
Matlab线性规划实例
优化目标：
- 生长最快（生物量biomass最大）
- 某代谢物(ATP、次级代谢物)产量最大或最小（致死）
应用
生长速率模拟预测
次生代谢产物最大化
微生物致死的研究（抗生素研发）
动植物特定组织或发育过程中特定阶段的代谢分析等
流程
构建代谢网络
把代谢网络表示成计量学矩阵
基于稳态假设，根据物料平衡，得到线性方程组（即约束条件）
定义优化目标（函数）
求解约束下的优化问题，得到流分布和相应的目标值
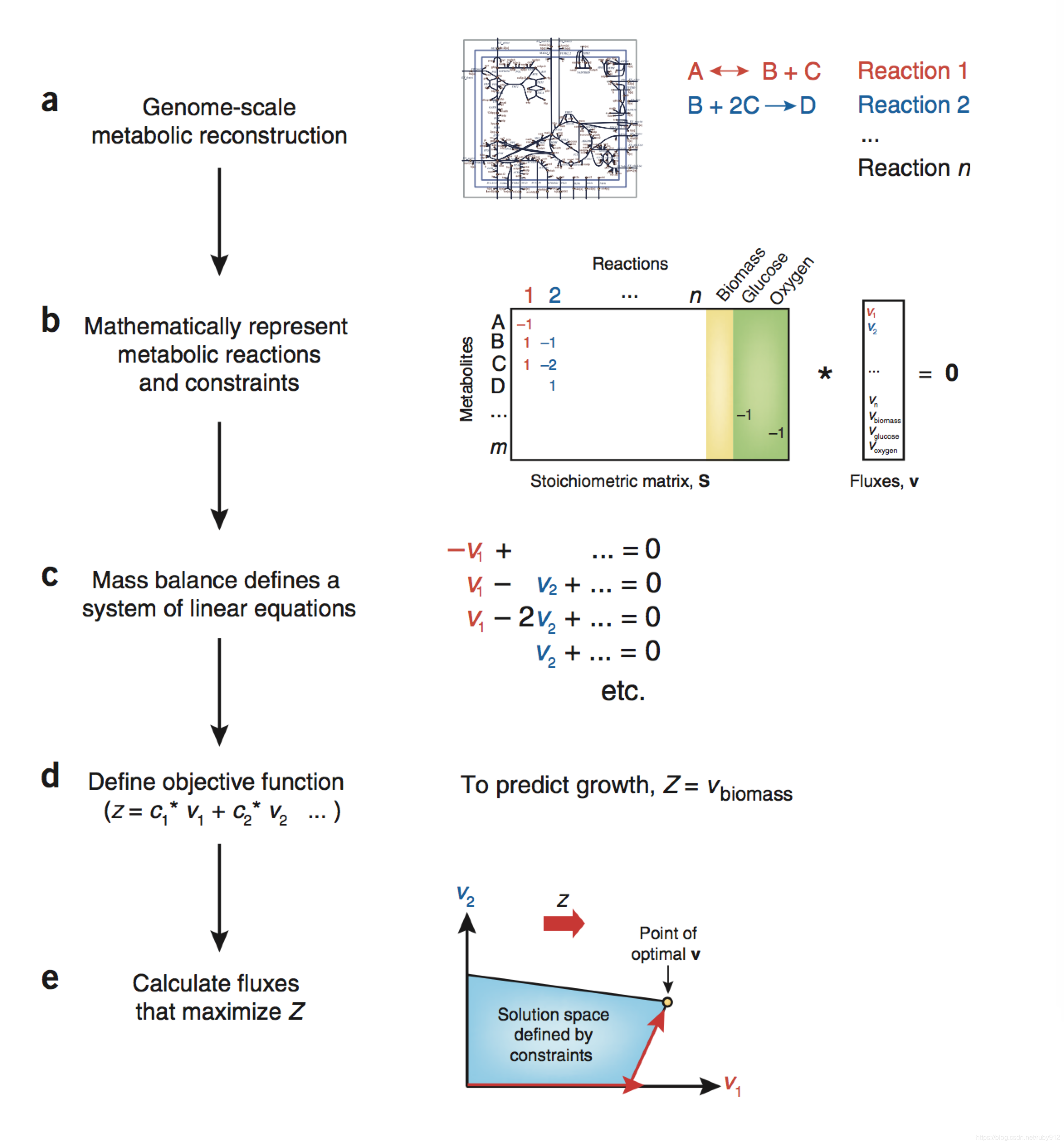图片来自文献：What is flux balance analysis? 2010
此处补充：线性代数笔记2――向量（向量简介）
示例
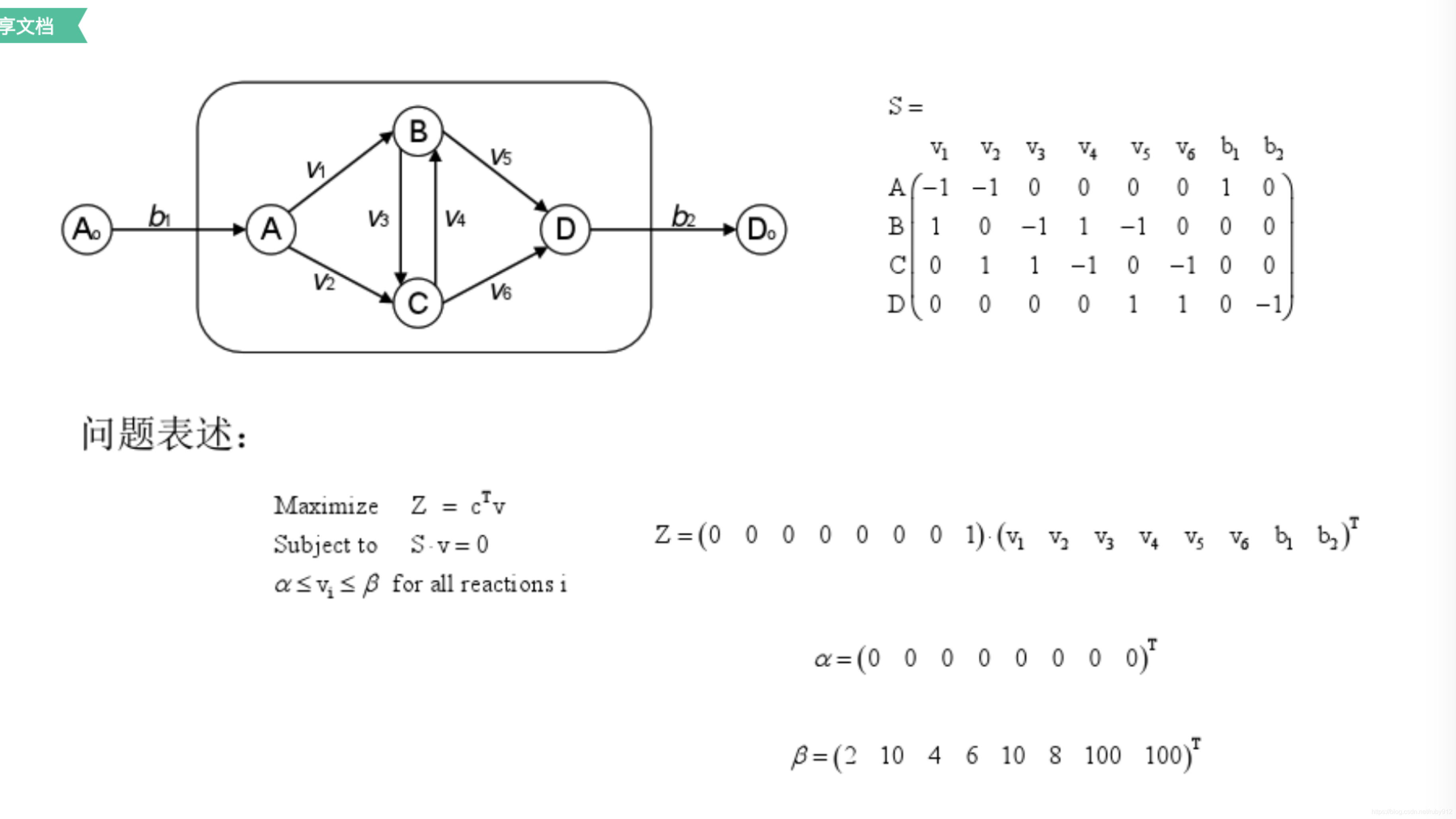
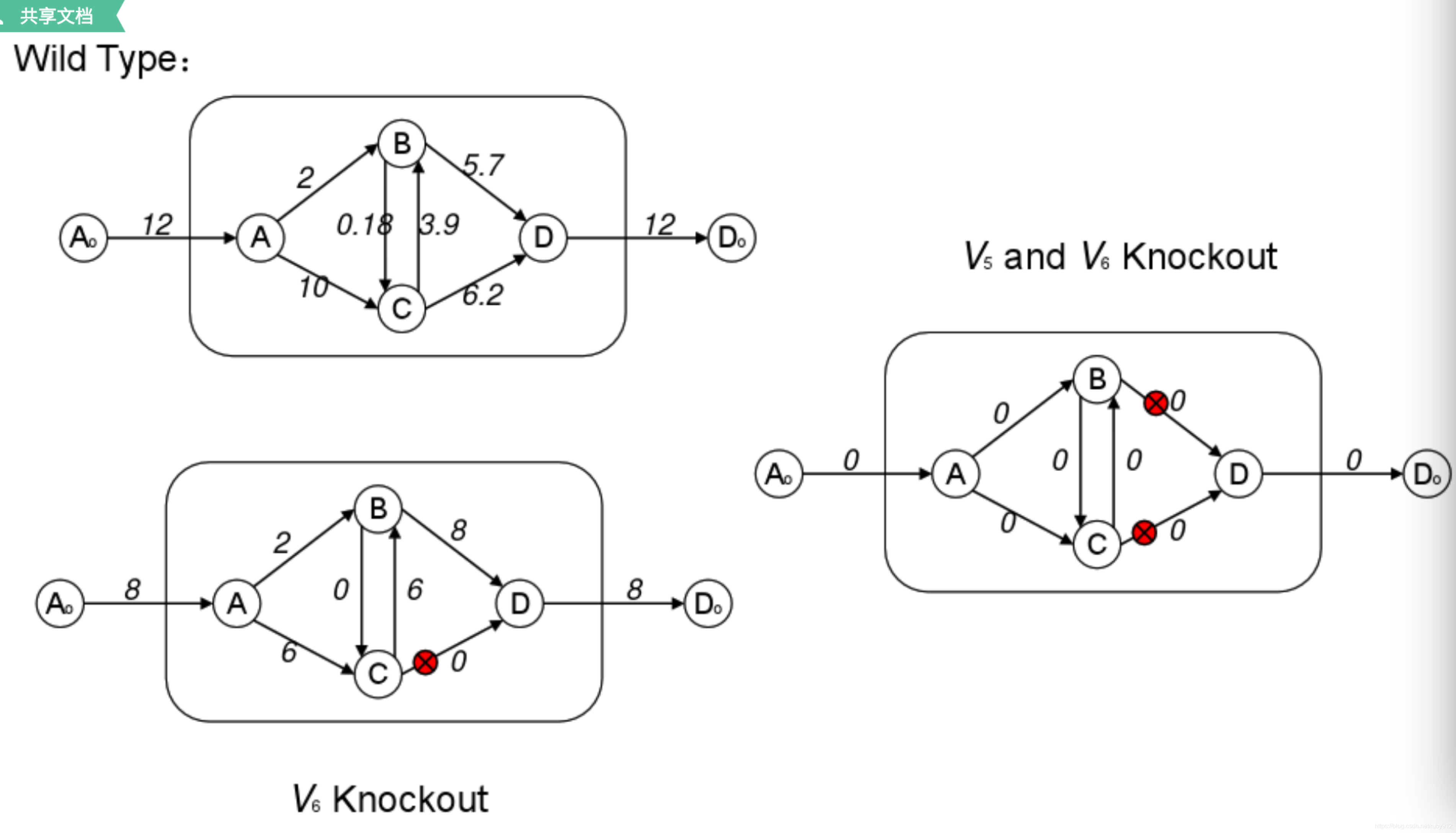
经典文献（里程碑）
FBA模型的提出(AEM-Varma1994)
DFBA模型的提出(BioPhysiJ-Mahadevan2002)
MOMA模型的提出(PNAS-Segre2002)
M_DFBA模型的提出(MSB-Luo2006)
idFBA模型的提出(PlosCB-Lee2008)
文章来源: https://blog.csdn.net/ruby912/article/details/91398842