基于四阶贝塞尔曲线的无人驾驶可行轨迹规划
背景
对于实际的无人车系统来说, 轨迹规划需要保证其规划出来的轨迹满足运动学约束、侧滑约束以及执行机构约束。为了生成满足无人车初始状态约束、目标状态约束的局部可行轨迹, 提出了一种基于四阶贝塞尔曲线的轨迹规划方法. 在该方法中, 轨迹规划问题首先被分解为轨形规划及速度规划两个子问题.。为了满足运动学约束、初始状态约束、目标状态约束以及曲率连续约束, 由3 个参数确定的四阶贝塞尔曲线来规划轨迹形状。
采用四阶贝塞尔曲线的优点
1、本文提出的轨迹规划方法是基于四阶贝塞尔曲线的, 其生成的轨迹满足运动学约束, 并且轨迹以及轨迹曲率是连续的。
2、本文生成的轨迹曲率是有界的.该边界由无人车的转向能力确定, 从而保证该轨迹对转向机构来说是可行的。
3、 本文生成的轨迹速度及加速度是连续的, 并且加速度是有界的。
4、 本文提出的轨迹规划方法对参数初值是不敏感的, 不需要预先存储参数与状态的对应关系。
问题描述

其中曲率、转弯半径、前后轮轴距以及前轮转向角之间的关系:

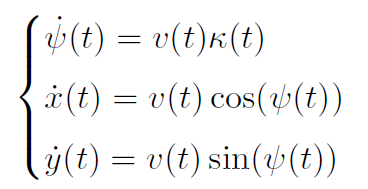
四阶贝塞尔曲线
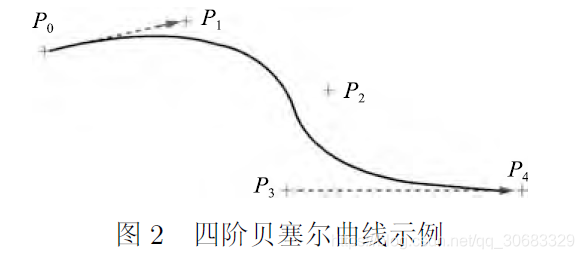
如图所示:这个四阶贝塞尔曲线是一个由5个控制点确定的唯一平面曲线。其参数化表达式为: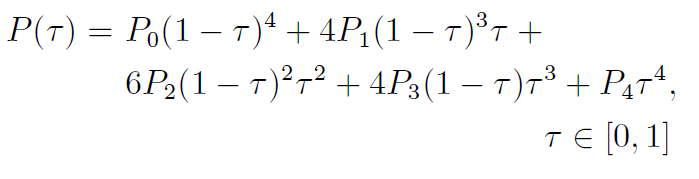
其中四阶贝塞尔曲线一定会从起点出发,到终点截止,因此一定会路过第一个和第五个控制点。
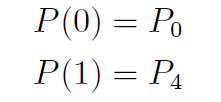
其曲线的切向量为: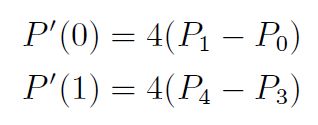
其中曲线曲率公式为: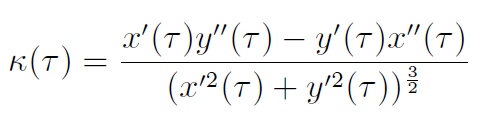
因此,其曲线在初始端点的曲率为: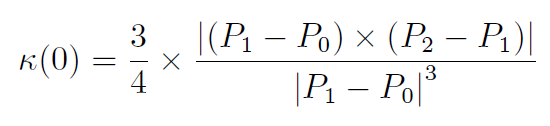
此外曲线具有仿射变换不变的特性。
轨迹生成算法
将无人车的速度控制和转向控制解耦剥离开,其相对时间的线速度和距离曲率为: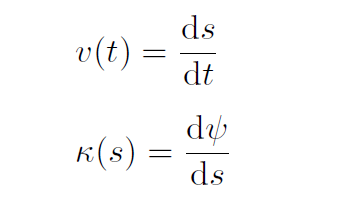
将这些公式代入: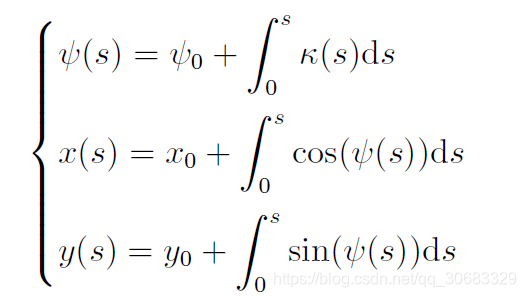
因此无人车的轨迹形状以及无人车在各点的航向角仅与无人车的移动距离以及在不同距离的曲率(前轮转向角) 有关. 在无人车不发生侧向滑动的条件下, 无人车速度仅影响完成该轨迹所消耗的时间。
所以可以把整个规划分为两个步骤:
1、生成合适的曲率,规划处满足初始状态的轨迹;
2、生成合适的速度,用以执行生成的轨迹;
同时为了保证这个轨迹是可用可执行的,需要满足一定的条件,主要是无人车运动学的约束:
1、曲率满足车辆动力学约束;
2、车体在s=0和s=st的时候的状态,要分别是X1和Xt;
3、为了保证连续的前轮转向角,k(s)应该是连续的;
4、为了保证转向机构可执行该轨迹,k(s)应该要有对应的无人车的界限;
其速度规划则有以下约束:
- 速度及加速度连续;
- 无人车以该速度执行该轨迹不会发生侧向滑动;
- 为了保证无人车可执行该速度, 应有界, 该界限由无人车加速能力决定.
轨迹规划
为了简化数学推导过程, 首先对初始状态的无人车进行旋转平移, 使得XI = [0 0 0 ・Ki]T. 由平面贝塞尔曲线的仿射变换不变的特性可知, 该旋转平移不会影响曲线的形状. 四阶贝塞尔曲线可以通过满足初始状态以及目标状态进行参数化.
1、初始状态约束Xs(0) = XI
初始状态的位置约束可以简单地通过设置第1个控制点P0 = (0; 0) 来满足. 设d1 = |P0P1|, 那么为了满足初始航向角约束, 由贝塞尔曲线的端点切向量特性可以得到第1个控制点的坐标为: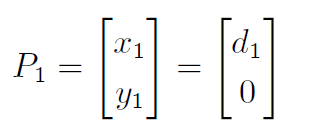
为了满足贝塞尔曲线在第1 个控制点的曲率约束Ki , 第2个控制点的坐标为: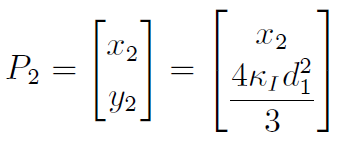
目标状态的位置约束可以通过设定P4 = (xT ,yT ) 来满足. 设d4 = |P3P4|, 为了满足目标状态的航向角约束, 第4 个控制点的坐标应为: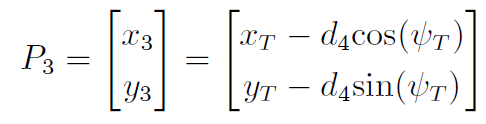
以上推导过程已满足无人车的初始状态及目标状态的约束, 同时得到了四阶贝塞尔曲线的5个控制点坐标. 这5个控制点中仅有3 个自由变量p =(d1, d4, x2), 即这3 个自由变量可以唯一确定5 个控制点, 进一步可以唯一确定该四阶贝塞尔曲线。
Matlab绘制
